Существует еще один метод для вычисления объема куба, который включает использование диагонали одной из его граней. Формула для нахождения объема куба через диагональ граней имеет такой вид:
Объем куба

В данном материале я расскажу о ключевых этапах работы над курсовой работой, а также о приемах, которые значительно упрощают процесс написания. У меня есть опыт самостоятельного написания курсовых, а также помощи другим студентам в этом вопросе. Моя основная рекомендация — обсудить любые проблемные моменты с вашим научным руководителем. Это особенно полезно в том случае, если вы уже знакомы с ним, например, если он ведет у вас занятия. Поддерживание контакта с научным руководителем поможет избежать необходимости вносить изменения в работу в последний момент.
Кубом называется трехмерная геометрическая фигура, имеющая одинаковые длины рёбер, где длина ребра (обозначенная как l) равна ширине и высоте.
Эта фигура также известна как гексаэдр, что определяет его как правильный многогранник, который состоит из квадратных граней. Куб имеет 6 граней, каждая из которых представляет собой квадрат, и все углы между гранями — прямые.

Формула объема куба
В геометрии многогранник, в том числе куб, имеет восемь вершин и шесть боковых граней. Дополнительно, иногда его могут называть призмой или параллелепипедом. По своей структуре куб содержит двенадцать рёбер, которые являются сторонами его граней. Всего существует четыре сечения, проходящие через центр куба и перпендикулярные основным рёбрам, которые соединяют две вершины параллелепипеда (в частности, правильные шестиугольники). Сумма квадратов этих рёбер составляет шесть. Углы, находящиеся в каждой верхней точке конструкции, суммируются до 270 градусов. Для вычисления объема V куба существует специальная формула.
Пример
В кубах длины, ширина и высота одинаковы. Умножение длины на ширину и высоту достаточно легко заменить возведением длины ребра в третий степень. Запись объема куба будет представлена как Vкуб = a³, где a — это длина стороны (рёбер). Например, чтобы определить объем куба при условии, что длина рёбер составляет пять сантиметров, следует выполнить следующие вычисления:
Что такое объем куба в геометрии
Куб — это пример правильного многогранника, у которого каждая грань представляет собой квадрат, а каждый угол между ними составляет 90 градусов. Эта фигура имеет множество интересных математических свойств, что делает ее объектом изучения в курсах геометрии.
Объем куба определяется как число пространства, занимаемое этим трехмерным объектом.
Объем записывается как положительное число и измеряется в кубических единицах, таких как кубические метры (м³), кубические сантиметры (см³) или кубические миллиметры (мм³) и других единицах измерения.
Полезная информация об объеме куба
| Единичный куб | Это куб, у которого длина ребра равна 1 единице, а площадь каждой грани — 1 квадратной единице. Единичные кубы широко используются для измерений объема различных предметов, начиная от жидкости и заканчивая твердыми объектами. Объем такого куба соответствует количеству единичных кубов, которые могут быть вместимы в более крупных кубах. |
| Кубометр | Кубометр представляет собой объем куба со стороной 1 метр. Это единица измерения объема в Международной системе единиц (СИ), и для удобства физики объем зачастую измеряют именно в кубических метрах (м³). |
| Может пригодиться | Соотношение объемов двух кубов определяется как куб коэффициента подобия. Определение выглядит следующим образом: V1/V2 = k³, где k — это коэффициент подобия. |
При решении любой задачи следует выделить данные из условия, которые помогут вам применить соответствующую формулу. Чтобы найти объем куба, можно использовать одну из следующих формул.
Объем куба через ребро
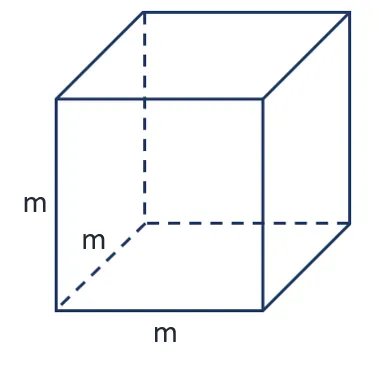
Длина всех рёбер у куба одинакова, давайте обозначим эту длину как m.
Тогда объем можно вычислить по формуле: V = m • m • m = m³.
Итак, V = m³
Объем куба через площадь полной поверхности
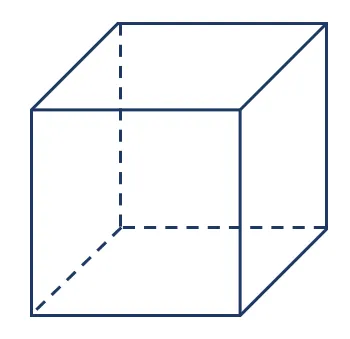
Поскольку у куба все грани квадратные, а их количество равно 6, площадь полной поверхности куба будет рассчитана по формуле: Sполн = 6 • m².
Теперь выразим m из этой формулы:
Подставим полученное значение m в формулу для расчета объема V = m³:
Где можно применить калькулятор
Калькулятор объема куба может быть использован в различных областях, где необходимы расчеты кубической формы. Вот некоторые из таких областей:
- ? Строительство. Строители могут использовать калькулятор объема куба для определения объема кубических зданий, бетонных блоков или кирпичей и других материалов, применяемых при строительстве.
- ? Производство. Калькулятор объема также может быть полезен в производственных процессах для анализа объема материалов, таких как металл, пластик или стекло, используемых в производстве кубических изделий.
- ? Логистика. Работа с калькулятором объема куба может помочь при планировании грузоперевозок, обеспечивая понимание того, сколько грузовых мест сможет вместить транспортное средство.
- ? Образование. Учителя математики в учебных заведениях могут применять калькулятор объема куба для образовательных целей с целью объяснения геометрии и расчетов объемов кубических форм.
- ? Интерьер и дизайн. Дизайнеры интерьеров могут использовать калькулятор для расчета объема кубических предметов, таких как шкафы, полки, столы и других элементов дизайна.
- ?️ Ремонт и обслуживание. В рамках ремонта и обслуживания калькулятор объема поможет определить необходимое количество материалов для замены или ремонта кубических элементов, таких как плитка, обои и прочее.
? Как посчитать объем куба
Объем куба можно легко вычислить самостоятельно, используя общепринятую формулу
где V — это объем куба, а a — длина его ребра.
Для проведенного вычисления объема куба необходимо измерить длину одного из рёбер с помощью линейки или любого другого измерительного инструмента. После этого следует возвести полученное значение в куб с помощью калькулятора либо произвести расчеты вручную.
Например, если длина ребра куба составляет 5 сантиметров, тогда объем куба будет равен V = 5³ = 125 кубических сантиметров.
Важно учитывать, что все единицы измерения должны быть согласованы. То есть, если длина ребра указана в сантиметрах, то объем также должен быть представлен в кубических сантиметрах.
? Часто задаваемые вопросы

1️⃣ Что такое куб и как он выглядит?
Куб — это трехмерное геометрическое тело, имеющее шесть равных граней, каждая из которых представляет собой квадрат. Все грани куба соединены под прямыми углами. Визуально куб можно представить как квадратный ящик.
2️⃣ Как найти объем куба?
Объем куба можно вычислить с использованием формулы V = a³, где V означает объем, а a — длину одной из сторон куба. Проще говоря, чтобы рассчитать объем куба, необходимо возвести длину его стороны в куб.
3️⃣ Каковы единицы измерения объема куба?
Объем куба традиционно измеряется в кубических единицах длины, таких как кубические сантиметры (см³), кубические метры (м³) или кубические дюймы (in³), в зависимости от используемой системы измерений в конкретной ситуации.
4️⃣ Как объем куба связан с его длиной стороны?
Объем куба прямо пропорционален длине одной из его сторон. Это означает, что если увеличить длину ребра в два раза, объем куба возрастет в восемь раз. К примеру, куб со стороной 2 см имеет объем 8 см³, а куб со стороной 4 см — объем 64 см³.
5️⃣ Какие приложения имеет объем куба в реальной жизни?
Расчет объема куба находит широкое применение в практике. Например, при планировании хранения предметов в коробках или контейнерах важные данные о объеме помогают определить, сколько объектов может быть размещено в конкретном объеме. Также, при проектировании зданий или конструкций расчеты объема помогают определить количество требуемых материалов, таких как кирпичи или бетон.
6️⃣ Какое значение имеет объем куба в математике?
Понимание объема куба является критически важным понятием в математике и связано с идеей трехмерного пространства. Расчет объема куба может быть применен к другим объемным фигурам, таким как призмы и цилиндры, что имеет практическое значение в таких областях, как физика и инженерия.
Куб считается одной из самых простых и широко изучаемых объемных фигур в геометрии. Расчет объема куба становится одним из первых математических навыков, с которым знакомятся учащиеся в школе, и это важный шаг к более глубокому пониманию сложных понятий объема и трехмерного пространства в математике и смежных науках.
Определение и основные свойства
Одним из наиболее значимых свойств куба является его объем, который можно определить с помощью формулы. Рассмотрим это подробнее.
Каждая сторона куба представляет собой одно из трех измерений. Например, если длина ребра куба составляет 5 сантиметров, это также означает, что его ширина и высота равны 5 сантиметрам. Или, если длина ребра составляет 10 сантиметров, то ширина и высота тоже будут равны 10 сантиметрам. Таким образом, все стороны куба взаимосвязаны и равны между собой.
Формула для вычисления объема куба

Когда мы приступаем к строительству, например, кладем кирпичную стену, важно подсчитать, сколько кирпичей потребуется для ее возведения. Но что если вместо стены мы хотим определить объем однородного куба? Как узнать, сколько именно материала нам нужно для его конструирования? Этот процесс оказывается довольно простым и доступным для понимания!
Формула для вычисления объема куба учитывает все основные характеристики этой геометрической фигуры. Прежде всего, необходимо помнить, что у куба одинаковые стороны, поэтому для нахождения объема не стоит применять классическую формулу для прямоугольного параллелепипеда. Вместо этого нужно использовать уникальную формулу, которая основана на равенстве всех рёбер.








