В нашем эксперименте будет три разных проводника, каждый из которых имеет отличные значения сопротивления. Мы будем подключать их по очереди к электрической цепи, и после каждого подключения будем записывать показания амперметра.
Формула закона Ома
Закон Ома был открыт Георгом Омом на основе различных экспериментов. При создании вольт-амперной характеристики для проводника можно наблюдать, что сила тока (I), протекающего через проводник, прямо пропорциональна напряжению (U), приложенному к нему, что можно записать как $(I \sim U)$.
Если в рассматриваемом участке цепи, содержащем проводник, нет источников электродвижущей силы (ЭДС), то формула закона Ома становится максимально простой и принимает следующий вид:
где R – это сопротивление проводника или же комбинации проводников, составляющих данную часть цепи.
Когда на этот участок цепи подключен источник тока, который задается через ЭДС ($\varepsilon$), то формула закона Ома претерпевает некоторые изменения:
Формула закона Ома в дифференциальной форме
Все ранее упомянутые формулы закона Ома были представлены в интегральной форме. Однако этот закон можно также записать в дифференциальной форме, которая иллюстрирует электрическое состояние в определенной точке проводящей среды.
где $\sigma=\frac$ – удельная проводимость, $\rho$ – удельное сопротивление, $\bar{J}$ – вектор плотности тока, $\bar{E}$ – вектор напряженности электрического поля. Векторы $\bar{J}$ и $\bar{E}$ описывают состояние в одной конкретной точке проводящей среды. В том случае, если среда является изотропной, то $\bar{J} \uparrow \uparrow \bar{E}$, что означает, что векторы направлены в одном направлении.
Отдельный участок и полная электрическая цепь
Рассматривая электрическую цепь в контексте применения закона Ома, важно учесть два варианта расчета: аналитику отдельно взятого участка цепи и полноценной электрической схемы в целом.
Расчет тока участка электрической схемы
Под участком электрической цепи обычно понимается специфическая часть схемы, исключающая источник ЭДС, поскольку он вносит дополнительное внутреннее сопротивление.
Поэтому формула для расчета тока в данном случае выглядит следующим образом:
I = U / R,
Здесь трактовка формулы довольно простая: ток, проходящий через определенный участок цепи, пропорционален напряжению, приложенному к этому участку, и обратно пропорционален сопротивлению, воздействующему на него.
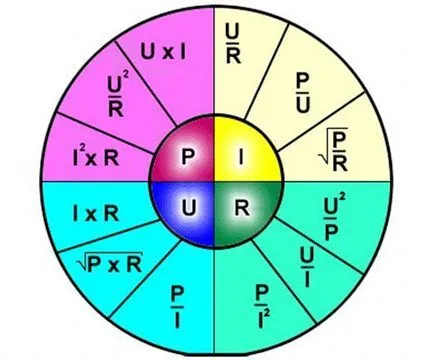
Представленная графическая схема, известная как графическая ромашка, отображает все возможные вариации формулировок, которые базируются на законе Ома. Этот инструмент удобен для быстрого поиска нужной информации: сектор P содержит формулы мощности; сектор U включает формулы напряжения; сектор I охватывает формулы тока; сектор R отвечает за формулы сопротивления.
Таким образом, данная формула ясно демонстрирует зависимость протекания тока по конкретному участку электрической цепи от заданных значений напряжения и сопротивления.
Формула особенно полезна при расчетах параметров сопротивления, которое необходимо впаять в схему, если значения напряжения и тока уже известны.
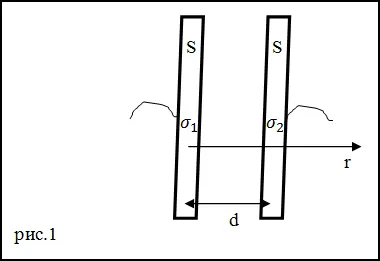
Закон Ома и два произведенных следствия, которыми должен быть знаком каждый профессиональный электромеханик, инженер-электрик, электронщик и все, кто работает с электрическими цепями. На рисунке слева направо: 1 — формулировка для нахождения тока; 2 — формулировка для нахождения сопротивления; 3 — формулировка для нахождения напряжения, где I – это сила тока, U – это напряжение, R – это сопротивление.
Представленный выше рисунок позволяет, например, определить ток, проходящий через резистор с сопротивлением 10 Ом, к которому приложено напряжение 12 вольт. Подставив известные данные, мы можем получить: I = 12 / 10 = 1.2 ампера.
Аналогичным образом можно решать задачи на поиск сопротивления (если известны ток и напряжение) или напряжения (если известны ток и сопротивление).
Таким образом, всегда можно сконструировать требуемое рабочее напряжение, необходимую величину тока и оптимально подобранный резистивный элемент для данной цепи.
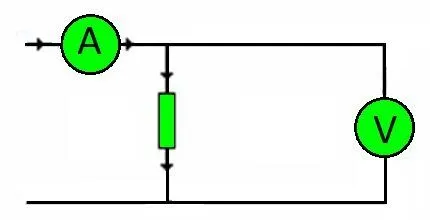
Формула, которая предлагается для использования, не требует учета параметров источника напряжения. Однако если схема содержит, например, аккумулятор, то расчеты будут производиться по иным правилам. В схеме: А – это подключение амперметра; V – это включение вольтметра.
Также следует отметить, что соединительные провода любой схемы представляют собой сопротивления. Размер нагрузки, которую они могут выдержать, будет определяться величиной приложенного напряжения.
Поэтому, применяя закон Ома, становится возможным точно подобрать необходимое сечение проводника в зависимости от материала, из которого изготовлены жилы.
На нашем сайте вы можете найти подробное руководство по расчету сечения кабеля в зависимости от мощности и тока.
Вариант расчета для полной цепи
Полная электрическая цепь состоит не только из участка (или участков), но и источника ЭДС. Это значит, что к существующему резистивному компоненту участка цепи добавляется внутреннее сопротивление источника ЭДС.
Последовательное и параллельное включение элементов
При работе с элементами электрической цепи (участками цепи) необходимо помнить, что их соединение может быть либо последовательным, либо параллельным.
В зависимости от типа соединения будет различаться и характер течения тока, а также способ подключения напряжения. Поэтому закон Ома также применим по-разному в зависимости от того, каким образом элементы подключены друг к другу.
Цепь последовательно включенных резистивных элементов
В случае последовательного соединения (при включении двух компонентов в цепь) используется следующая формулировка:
Эта формулировка четко показывает, что независимо от количества последовательно соединенных резистивных компонентов, ток, текущий через участок цепи, остается неизменным.
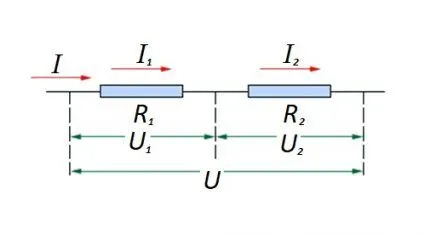
Соединение резистивных элементов последовательно друг с другом на участке схемы. Для данного варианта расчетов вводятся свои правила. На схеме: I, I1, I2 – это протекание тока; R1, R2 – это резистивные элементы; U, U1, U2 – это напряжения, приложенные к каждому из компонентов.
Общее величина напряжения, приложенного к всем резистивным компонентам цепи, равняется сумме напряжений на каждом элементе, что в итоге составляет общее значение источника ЭДС.
При этом напряжение на каждом отдельном компоненте определится по формуле: U_x = I * R_x.
Общая же величина сопротивления в таком случае вычисляется по формуле, которая представляется как сумма всех резистивных величин: R_total = R1 + R2 + … + Rn, где n – количество резистивных компонентов.
Цепь параллельно включенных резистивных элементов
Если в цепи осуществляется параллельное включение резистивных компонентов, то для данного случая справедлива следующее формулировка согласно закону Ома:
Не исключается возможность создания схем с комбинированным типом, когда используются как параллельные, так и последовательные соединения.
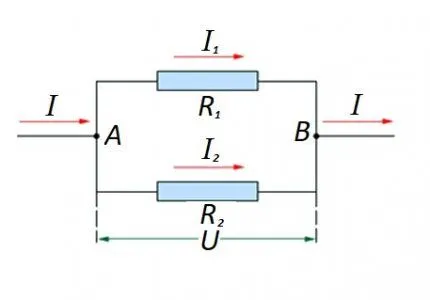
Здесь резистивные элементы соединяются параллельно друг с другом на отклонении от предыдущей схемы. Для этого варианта расчета применяется своя специфика. На данной схеме: I, I1, I2 – это величины протекания тока; R1, R2 – резистивные элементы; U – это подводимое напряжение; A, B – точки подключения.
При таких комбинациях расчет обычно начинается с определения эквивалентного сопротивления параллельного соединения. После получения результата к этому значению добавляется резистивный компонент, который включен последовательно.
Интегральная и дифференциальная формы закона
Все рассмотренные моменты касаются расчетов в ситуации, когда электрические схемы используют проводники однородной структуры.
Тем не менее, на практике часто возникают схемы, где на различных участках используется проводник с различной структурой. Например, могут быть задействованы провода с разным сечением, изготовленные из различных материалов.
Чтобы учесть такие различия, существует вариант так называемого дифференциально-интегрального закона Ома. Для бесконечно малого проводника рассчитывается величина плотности тока в зависимости от напряженности электрического поля и уровня удельной проводимости.
Для дифференциального расчета используется следующее выражение: J = σ * E.
Для интегрального расчета можно записать по формуле: I * R = φ_1 – φ_2 + έ.
Однако к этим примерам больше относятся учебные задачи высшей математики, и в реальной профессиональной практике простого электрика они, как правило, не применяются.
Как добиться понимания закона Ома?
Чтобы лучше интуитивно понять закон Ома, можно обратиться к аналогии, в которой ток представляется в виде потока жидкости. Так именно думал Георг Ом, когда проводил эксперименты, в результате которых был открыт закон, названный его именем.
Допустим, что ток равносилен движению потока воды в трубе. Вода сначала поднимается насосом на высоту, а оттуда, под действием потенциальной энергии, начинает течь вниз по трубе. При этом чем выше насос поднимет воду, тем быстрее она будет течь по трубе.
Следовательно, скорость потока воды (которая аналогична силе тока в проводнике) зависит от потенциальной энергии воды (разности потенциалов).
Сила тока прямо пропорциональна напряжению.
Теперь перейдем к сопротивлению. Гидравлическое сопротивление представляет собой сопротивление трубы, связанное с ее диаметром и шероховатостью стенок. Логично предположить, что чем больше диаметр трубы, тем меньше ее сопротивление, и соответственно, тем большее количество воды (больший ток) сможет пройти через диаметральное сечение.
Сила тока обратно пропорциональна сопротивлению.
Однако такую аналогию можно использовать в основном для базового понимания закона Ома, поскольку его исходная формулировка фактически является довольно грубым приближением, которое, тем не менее, находит отличное применение на практике.
На самом деле сопротивление вещества обусловлено колебаниями атомов в кристаллической решетке, тогда как ток представляет собой движение свободных носителей заряда. В металлах такими свободными носителями являются электроны, освобождающиеся от своих атомных орбит.
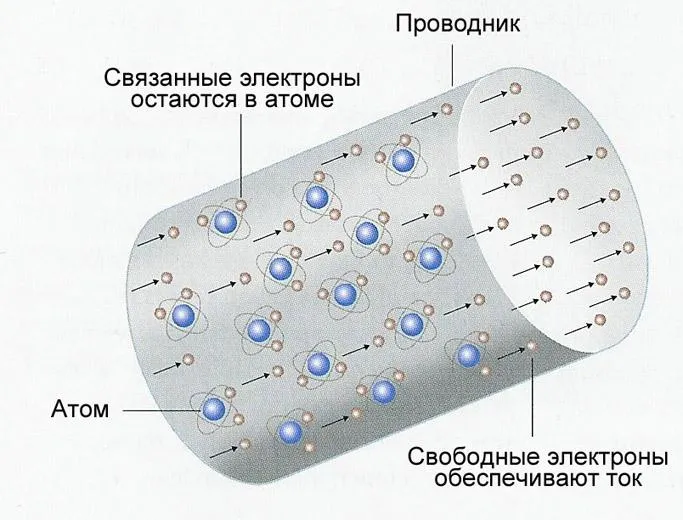
В данной статье мы стремились дать простое и ясное объяснение закона Ома. Понимание этих, на первый взгляд, простых принципов может оказать хорошую службу вам на экзаменах. Конечно, мы привели только самую простую формулировку закона Ома, не уходя при этом в сложные аспекты высшей физики, такие как активное и реактивное сопротивление и другие тонкости.
Если возникнет необходимость изучить данные темы более глубоко, сотрудники нашего студенческого сервиса готовы прийти вам на помощь. Также в завершение предлагаем вам ознакомиться с интересным видеоматериалом о законе Ома, который действительно может быть познавательным!
- Контрольная работа от 1 дня / от 120 р. Узнать стоимость
- Дипломная работа от 7 дней / от 9540 р. Узнать стоимость
- Курсовая работа от 5 дней / от 2160 р. Узнать стоимость
- Реферат от 1 дня / от 840 р. Узнать стоимость
Иван Колобков, также известный как Джони. Маркетолог, аналитик и копирайтер компании Zaochnik. Перспективный молодой писатель с интересом к физике, антиквариату и творчеству Ч. Буковски.
Навигация по статьям
- Оформление работ
- Отчет по практике
- Рефераты
- Дипломная работа
- Контрольная работа
- Курсовая работа
- Абитуриентам
- Студентам на заметку
- Выпускникам вузов/колледжей
- Поступление в колледж
- Рейтинги вузов России
- Подготовка к экзамену
- Обучение за рубежом
- Карьера для начинающих
- Самостоятельная работа
- Чертежи
- Презентации
- Эссе
- Иностранные языки
- Постдипломное образование
- Полезно знать
- Лайфхаки
- Генетика для «чайников»
- Математика для «чайников»
- Химия для «чайников»
- Экономика для «чайников»
- Биология для «чайников»
- Экология для «чайников»
- Физика для «чайников»
- Бухгалтерский учет и аудит для «чайников»
- Виды аттестаций
- Рецензия
Читайте разделы по теме
- Что такое фаза и ноль в электричестве
- Электрические цепи
- Факты о физике
- Материалы по физике различных направлений
- Основные формулы
- Задачи по физике
- Закон Ньютона
- Закон Ома
- Вид работы: Дипломная работа
- Время выполнения: 8 дней
- Стоимость заказа: 8 000 руб.
- Вид работы: Дипломная работа
- Время выполнения: 8 дней
- Стоимость заказа: 8 000 руб.
- Вид работы: Реферат
- Время выполнения: 3 дня
- Стоимость заказа: 1 000 руб.
- Вид работы: Презентация (PPT, PPS, Prezi)
- Время выполнения: 3 дня
- Стоимость заказа: 2 000 руб.
- Вид работы: Презентация (PPT, PPS, Prezi)
- Время выполнения: 2 дня
- Стоимость заказа: 1 500 руб.
Зависимость сопротивления от температуры
При повышении температуры сопротивление у большинства металлов увеличивается. Однако существуют сплавы, такие как константан и манганин, у которых сопротивление остается почти неизменным при увеличении температуры. В то же время сопротивление, наблюдаемое у электролитов, обычно уменьшается с повышением температуры.
Температурный коэффициент сопротивления проводника определяется как отношение величины изменения сопротивления проводника при температуре 400°С к его базовому сопротивлению при 0°С:
Зависимость удельного сопротивления проводников от температуры можно выразить с помощью следующей формулы:
Во общем случае $α$ зависит от температуры, но если температурный диапазон невелик, температурный коэффициент можно считать постоянным. Для чистых металлов $α=(/)K^$. Для растворов электролитов $α$.
Связь силы тока и сопротивления
После завершения всех измерений мы занесли результаты в таблицу 1.

Как формулируется закон Ома?
Сила тока в участке цепи прямо пропорциональна напряжению, приложенному к концам этого участка, и обратно пропорциональна его сопротивлению.
$I = \frac$,
где $I$ — сила тока в данной части цепи, $U$ — напряжение на концах этого участка, $R$ — электрическое сопротивление этого участка.
На графике по горизонтали отложены значения сопротивления проводников в омах, а по вертикали — величина силы тока в амперах.
Упражнения
Упражнение №1
На зажимах электрического утюга напряжение равно $220 \space В$, а сопротивление нагревательного элемента утюга составляет $50 \space Ом$. Определите силу тока в нагревательном элементе.
Дано:
$U = 220 \space В$
$R = 50 \space Ом$
Разработаем решение и ответ на задачу.
Решение:
Согласно закону Ома для данной части цепи: $I = \frac$.
Первым делом рассчитаем силу тока:
$I = \frac = 4.4 \space А$.
Ответ: $I = 4.4 \space А$.
Упражнение №2
Сила тока в спирали электрической лампы составляет $0.7 \space А$, а сопротивление лампы равно $310 \space Ом$. Найдите напряжение, при котором работает лампа.
Дано:
$I = 0.7 \space А$
$R = 310 \space Ом$
Разработаем решение и ответ на задачу.
Решение:
Согласно закону Ома для этого участка цепи: $I = \frac$.
Теперь выразим напряжение и рассчитаем его:
$U = I * R$,
$U = 0.7 \space А \cdot 310 \space Ом = 217 \space В$.
Ответ: $U = 217 \space В$.
Упражнение №3
Каково сопротивление вольтметра, рассчитанного на $150 \space В$, если сила тока в нем не должна превышать $0.01 \space А$?
Дано:
$U = 150 \space В$
$I = 0.01 \space А$
Разработаем решение и ответ на задачу.
Решение:
Применим закон Ома для этого участка цепи: $I = \frac$.
Теперь выразим сопротивление и посчитаем его, используя максимальные значения напряжения и силы тока для устройства:
$R = \frac$
$R = \frac = 15,000 \space Ом = 15 \space кОм$.
Ответ: $R = 15 \space кОм$.
Упражнение №4
Определите сопротивление проводника, основываясь на графике (рисунок 4).
Воспользуемся данными из графика. При напряжении $10 \space В$ сила тока в проводнике соответствует $2.5 \space А$. Запишем условия задачи и решим ее.
Заметьте, что сопротивление $R$ не зависит ни от величины тока, ни от напряжения. Поэтому можно выбирать любые значения тока и напряжения из графика. Ответ останется неизменным.
Дано:
$U = 10 \space В$
$I = 2.5 \space А$
Разработаем решение и ответ к задаче.
Решение:
Согласно закону Ома для данной части цепи: $I = \frac$.
Теперь выразим сопротивление и рассчитаем его значение на основе данных из графика:
$R = \frac$,
$R = \frac = 4 \space Ом$.
Ответ: $R = 4 \space Ом$.
Упражнение №5
Рассмотрите рисунок 1 и таблицу результатов эксперимента, произведенного в соответствии с этим рисунком. Что произойдет с рисунком и схемой электрической цепи при проведении опытов №2 и №3, указанных в таблице 1?
Для опыта №2:
к рисунку будет подключен другой проводник с сопротивлением $3.5 \space кОм$. Амперметр будет отражать силу тока равную $0.4 \space A$.
Для опыта №3:
в схеме ничего не изменится. Это иллюстрация именно этого опыта (в цепь включен проводник с сопротивлением $4 \space Ом$).
Схема электрической цепи останется одинаковой для всех трех опытов, если не учитывать сопротивление проводника (как показано на рисунке 5).
Упражнение №6
Определите сопротивление проводника AB, исходя из показаний приборов (рисунок 6).
Дано:
$U = 4 \space В$
$I = 1 \space А$
Разработайте решение и ответ на задачу.